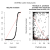The latest update of the DHARMa R package (0.4.6) includes an option to perform simulated likelihood ratio tests (LRTs) for GLMMs based on a parametric bootstrap. I wanted to shortly comment on how this works and why this is useful.
Why is this useful?
A well-known issue with mixed models is that the df lost for a random effect (RE) depend on the fitted RE variance, which controls the freedom (or conversely, the shrinkage) of the RE estimates. As a consequence, the df lost by a RE a not fixed a priori, but have to be estimated after fitting the model (adaptive shrinkage). One could add that even on a more fundamental level, the df implies that the null distribution is fixed (e.g. chi2) in the first place, which is also not entirely true in a non-asymptotic case.
As a consequence, ANOVA and AIC functions with naive df calculations should not be used for selecting on variance components of mixed models, and in principle, the problem can permeate to the fixed effects as well (if those change the RE df). Unfortunately, the options to calculated corrected df in R are relatively limited – the most common choice is the lmerTest package, which uses the Satterthwaite approximation, but this only works for linear models.
Simulated LRT as a a non-parametric alternative
An alternative to a parametric tests (which requires df) is a simulated LRT based on a non-parametric bootstrap. The idea for this is very easy:
- As for any LRT, we have two models M0 nested in M1, H0: M1 is correct, and we want to use the test statistics of log LR(M1/M2).
- However, instead of trying to get a parametric expectation for the test statistic under H0, we simply simulate new response data under M0 (parametric bootstrap), refit M0 and M1 on this data, and calculate the LRs. Based on this, calculate p-values etc. in the usual way.
In principle, this should give you correct p-values for any LRT / ANOVA calculation that compares between (nested) model alternatives, regardless of whether those nested alternatives differ in fixed or random effects. I had often used this trick by hand, but it did occur to me that it would be very simple / useful to implement this in DHARMa, because DHARMa already implements wrappers for simulations and refitting of models for a wide range of GLMM functions in R.
Practical example
OK, let’s see how this would work in practice: here’s the example for the function in the DHARMa package. Note that we simulate data with a relatively strong RE
library(DHARMa)
library(lme4)
# create test data
set.seed(123)
dat <- createData(sampleSize = 200, randomEffectVariance = 1)
# define Null and alternative model (should be nested)
m1 = glmer(observedResponse ~ Environment1 + (1|group), data = dat, family = "poisson")
m0 = glm(observedResponse ~ Environment1 , data = dat, family = "poisson")
# run LRT - n should be increased to at least 250 for a real study
out = simulateLRT(m0, m1, n = 10)
The result that we get is:

We also get (per default, can be switched off) a graphic representation of the simulated null distribution: